應該是太容易就把分數類型及轉換的程式給寫好,加料的壞習慣又來了,想說應該要有分數計算的部份才對吧!想不到這個念頭又讓自己陷入很損耗腦細胞的程式碼漩渦中…想起來很簡單自然的事情,在實現面常常都是複雜的…※不是艱難而是複雜!
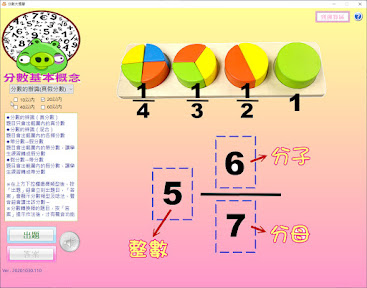
我在這支程式的畫面中,用了許多「憤怒鳥」的圖,它是我女兒小時候很喜歡的卡通人物,※這組Angry bird的圖是取自https://snap2objects.com/ (https://creativecommons.org/licenses/by/3.0/)而程式的icon及裡頭的關於頁用的Garfield,則是我個人很喜歡的,用的圖也是我女兒小時候手繪的~
趁此機會讓畫面有點樂趣
在寫分數的加減乘除這個部份,比較費神的加減的部份,主要是因為分母通分的部份,還有讓電腦亂數出題,有可能會出一些答案是負數的,這個在小學可是不適用的…
還有,我不僅想讓程式自己出題、自己給出答案,還希望它能列出建議的計算過程,最後也能有語音講出來的功能,這些都是費功的地方,一時間開始思考分數的SOP算法是我個人的收獲…發現在這些計算中,求二數的「最大公因數」的能力非常重要,所以五年級的課程中,因數這個話題,小朋友一定要學好…
在程式中,我就要先寫一個取最大公因數的演算式才行,找了一下資料最棒的方式應該是「輾轉相除法」又稱歐幾里得算法(英語:Euclidean algorithm),而在中國則可以追溯至東漢出現的《九章算術》(幾千年前的人智慧怎麼如些高呀!)
我實作出下列CODE
--求最大公因數
function gcd(m,n)
local remainder = Math.Mod(m, n);
while remainder ~= 0 do
m = n;
n = remainder;
remainder = Math.Mod(m, n);
if remainder == 0 then
break;
end
end
return n;
end
--求最小公倍數
function lcm(m,n)
local product = m*n;
local gcd_n = gcd(m,n);
return product/gcd_n;
end
因為 二數乘積 = 最大公因數*最小公倍數,所以找出最大公因數後,鐵定能算出最小公倍數。在程式中需要二個數字,就把原始值送進涵數去,不過要避開0,否則程式就可能會掛掉了…
在避開負數這個問題方面,則是善用了While迴圈:
n2x = Math.Random(min_num, max_num);
n3x = Math.Random(min_num, max_num);
while n2x < n3x do
n2x = Math.Random(min_num, max_num);
n3x = Math.Random(min_num, max_num);
if n2x > n3x then
break;
end
end
在程式中若希望亂數產生的n2x必須大於n3x,就判斷一下,萬一不是這樣就進入while巡迴中重跑到合適再跳出